RealTime_Rendering_4(1)—

1.1 内容简介
1.2 符号和定义

1.2.1 数学符号
1.2.2 几何定义
1.2.3 着色

更多资源

实时渲染的核心为：使用计算机快速绘制图片，使用者与屏幕中的图片进行交互，交互的结果直接影响到下一帧绘制的图片。这种交互和绘制的循环以足够高的频率进行着，使得使用者沉浸在一个动态的过程中，而不会意识到这是一张张独立的图片。它是计算机图形学中最具交互的领域。

图片显示的频率以FPS（frames per second）或者HZ（Hertz）为单位。如果渲染的速度为1FPS，则毫无交互可言，用户将会持续的很痛苦的等待下一张图片的到来。当达到6FPS的时候，开始慢慢有一些想去交互的感觉。视频游戏FPS的目标为30、60、72升至更高，当达到这种频率的时候，用户将会集中精神进行交互了。

电影每秒显示24帧图片，但是它会使用一个快门系统（shutter system）将每帧图片显示2-4次，用于防止出现闪烁。这样的话，刷新率也就和显示率（display rate）就独立开来，故使用HZ来表示。比如：快门系统如果将每帧图片显示3次，则刷新率为72HZ。液晶显示器（LCD）也将刷新率和显示率拆分看待。

Patrick：这里提到了几个概念（刷新率、显示率），从而引发了如下问题。问题1：同样的图片显示2-4次，为什么能防止闪烁？思考：首先，站在观察者的角度思考，他看到了什么。比如，观察者看到一秒连续显示24张不同内容的图片，每看到一张图片的时候，这张图片将在大脑留下印象，然后看到下张图片的时候，自动将和上一张图片进行关联，脑补出这两张图片中间的插值。然后，想下同样的图片显示1次和显示2-4次对观看者的区别，那么，其实从内容上是没有区别的。所以，从这个角度考虑这个问题是不对的。那么，就从另外一个角度考虑，传统的CRT（阴极射线管显示器）是通过高压高速电子束，轰击屏幕内荧光粉发光。那么如果刷新率比较低，比如1HZ，屏幕的亮度在这一秒内就会从亮到暗，然后再下一秒又从亮到暗，所以，这样就比较容易理解，提高刷新率可以防止闪烁了。（70Hz的刷新频率是在显示器稳定工作时的最低要求。一般建议85Hz）。但是，液晶显示器(LCD)的发光原理与传统的CRT是不一样的，由于液晶显示器每一个点在收到信号后就一直保持那种色彩和亮度，恒定发光，所以刷新率对CRT的意义比较突出，而对LCD来说，刷新高了，反而会影响其使用寿命，一般保持在60-75就可以了。

24FPS对于看视频来说，基本可以接受。但是为了降低延迟（反应时间）必须提高频率，因为15ms的延迟就足以减慢和干扰交互（参考文献[1849]），比如头戴式VR设备的要求为90FPS，以降低延迟。

Patrick：这里提到了一个概念（延迟），从而引发了如下问题。问题2：延迟是如何计算的，以及如何避免？思考：这个问题和游戏类别相关。单机游戏：会在一帧的开始获取到用户的输入，然而经过一系列的计算和渲染，当前帧将画面显示出来（比如Cocos2d-x，据说Unity也这么做了，尚未验证），这样的话延迟为一帧。网络游戏：用户输入后，会将数据传输给服务器进行验证（以防外挂），验证后再将信息传给客户端，按照上述单机游戏的时间轴进行处理。那么这里的延迟还要加上网络延迟。所以，避免的方式，只能是换个更好的设备，换个更好的网络了。所以，总的来说，延迟=一帧的时间+网络延迟。开发者能控制的，只能是提高帧率了。 FPS、moba等游戏帧率一般要求60，比如王者荣耀界面上时刻显示着当前的延迟（这个延迟包括网络延迟）。

然而，实时渲染的重点依然在渲染，而非交互。如果速度是唯一衡量标准，那么只需要根据用户输入随便在屏幕上绘制一些东西就足够了。显然这样是不行的，毕竟实时渲染主要还是用于渲染3D物件。

交互性和3D效果都是实时渲染的充分条件，另外还有第三个因素：图形硬件加速。1996年的3Dfx Voodoo 1 card开启了消费者层面的3D图形。随着市场的快速发展，现在每个电脑、平板、手机都自带图形处理器。正是由于这些硬件加速，才使得实时渲染这些精美的demo成了现实。

正是硬件的发展，才快速推动了计算机图形学交互领域的发展。在这里，我们主要关注如何提高画面质量，并提升绘制速度，同时，也会聊一下加速算法和图形API的特性和限制。我们可能无法深入覆盖到每个课题，我们的目的是告知大家关键概念和术语，解释业内最先进和最实用的算法，并指出在哪里可以获取到更多的信息。我们希望能通过这本书，给你带来理解这个行业的工具。

1.1 内容简介

下面为每个章节的简单介绍

2.图形渲染管线（The Graphics Rendering Pipeline）：实时渲染的核心。通过一套对场景的描述，一步步将所看到的内容绘制出来。

Patrick：在图形学里面其实有两种概念，都叫做渲染管线。这里我们要说的是底层的渲染管线，也就是如何通过CPU和GPU交互，设置状态机，如何创建并执行VS、PS等。而应用层的渲染管线，则是游戏行业熟知的前向渲染、延迟渲染等技术。

3.图形处理单元（The Graphics Processing Unit）：现代GPU中，使用一套固定函数（fixed-function）和可编程单元（programmable units）实现了渲染管线中的各个阶段
4.变换（Transform）：变换（Transform）是一套最基本的工具，用于控制位置、方向、尺寸、物件的形状、坐标系（location）以及摄像机的镜头视角等
5.着色基础（Shading Basics）：先讨论材质球和灯光，以及如何用它们来实现所需的表面外观（不管是写实还是风格化的）。然后介绍了一些和外观相关的主题，比如通过AA（antialiasing）、透明度、gamma矫正来实现更高质量的图片
6.纹理（Texturing）：实时渲染最强大的工具之一就是可以快速访问图片以及在物体表面显示图片。这个过程叫做纹理采样（texturing），有大量的方法用于实现它。
7.阴影（Shadows）：在场景中添加阴影可以增加真实感和感染力（comprehension）。这里会介绍用于快速计算阴影的最常用的算法。
8.灯光和颜色（Light and Color）：在聊基于物理的渲染之前，需要先理解如何量化光照和颜色。在PBS结束之后，需要将量化后的结果，根据屏幕的属性和观察到的环境，转换成数值用于显示。这两个课题在本章都会讲述。

Patrick：这里有个疑问，环境可以理解为环境光，屏幕的属性是什么...

9.基于物理的渲染（Physically Based Shading）；我们从头开始构建一个方便理解的PBS模型。本章从基础物理现象开始说起，使用包含各种渲染材质的模型，然后将它们渲染在一起，通过各种算法，在保留表面外观的同时，达到AA的效果
10.局部关照（Local Illumination）：描述复杂光源的算法。在这里，会认为光是由具有特殊形状的物理物件发射出来的。
11.全局光照（Global Illumination）：为了提高画面的真实感，通过算法模拟光照和场景之间的多次交互。在这里会聊一下环境光、方向光遮挡（directional occlustion）以及漫反射和高光反射渲染GI效果的方法，达到可以通过一个方案满足各种类型场景需求的效果。

Patrick：方向光遮挡（directional occlustion）是什么，类似于skyvisibility？那不就是shadow么...

12.后处理（Image-Space Effects）：图形硬件擅长快速的图像处理。先讨论图像过滤和重计算技术（reprojection），然后聊一些常用的后效：镜头光斑（lens flares）、运动模糊（motion blur）、景深（depth of field）。
13.使用多边形（Beyond Polygons）：三角形并非总是构建物件的最快/最真实的办法。使用基于图像、点云、体素（voxels）或者其他的方式都各有优点。

Patrick：这里有个疑问，ES可以绘制点、线、三角形，只有DX才能绘制polygon...那么基于体素只能..另外，基于图像是什么..

14.体渲染和半透明渲染（Volumetric and Translucency Rendering）：这里主要是说体渲染的理论，以及其与光源的交互。模拟的现象从大尺寸的大气散射到头发细纤维内的光散射
15.非真实渲染（Non-Photorealistic Renderin）：想要把一个场景绘制的真实，则只有一种渲染方法。而其他的风格，比如卡通风格或者水彩风格，在这里会介绍。除此之外，还会介绍线和文本生成技术

Patrick：线？是对应三角形的线么。文本生成是UI文本么..

16.多边形技术（Polygonal Techniques）：几何数据的来源很多，且数据量庞大，经常需要做一些调整使得渲染可以加速和提高质量。这里会介绍多边形数据展示和压缩的各种方法。
17.曲线和曲面（Curves and Curved Surfaces）：复杂表面可以在质量和渲染速度之间进行权衡，更紧凑的表示平滑曲面的生成
18.管线优化（Pipeline Optimization）：通过大量的优化技术可以将App更进一步提速（即便它已经使用了很有效率的算法了）。需要做的就是找到瓶颈并找到解决方案。这里还会讨论下多线程。
19.加速算法（Acceleration Algorithms）：功能完成后，就要进行优化。这里会讨论剔除和LOD渲染等方面的优化方案。
20.有效渲染（Efficient Shading）：大量的光照会影响性能，在确定一个物件是否可见之前就对其进行完全着色也是一种浪费。所以我们需要找各种办法解决之类渲染中的低效率。
21.虚拟现实和增强现实（Virtual and Augmented Reality）：在这个领域，想要快速一致的渲染真实图片，需要更有挑战性的特殊技术。
22.交叉测试（Intersection Test Methods）：交叉测试对于渲染、用户交互和碰撞检测非常重要。这里提供了常用的最有效的几何交叉试验算法。
23.图形硬件（Graphics Hardware）：这里介绍基本的架构类型、帧缓存（framebuffer）、颜色、深度。并对GPU的一个案例进行研究
24.未来（The Future）：随便聊聊
碰撞检测：鉴于篇幅的原因，碰撞检测一章被放到了网站http://realtimerendering.com上供免费下载，并附录上了线性代数和三角函数算法

Patrick：我一直认为，读完了一本书的前言，等于和作者做了一次从心出发的交流，了解作者写作时的状况和出发点，可以帮助更好的去理解一本书。而读完一本书的目录，相当于这本书已经读了1/3了，毕竟，如果看目录就能想到里面可能会涉及到的内容的话，那么这本书就基本在读者掌握中了。

1.2 符号和定义

首先，先聊一下书中出现的数学符号。如果想要更全面的了解本节以及本书中出现的术语，可以参考http://realtimerendering.com提供的线性代数附录。

1.2.1 数学符号

表1.1 总结了我们所使用的大多数数学符号。这里将详细介绍其中的一部分。

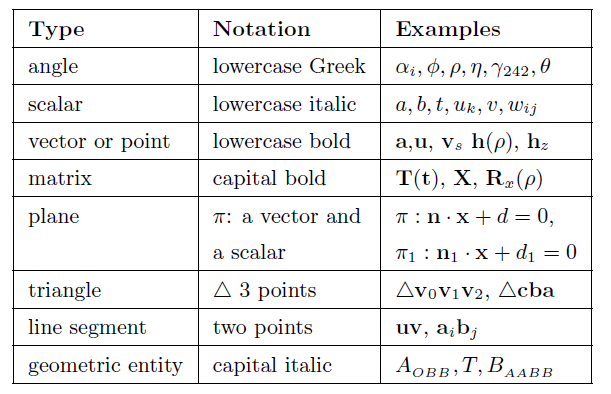
但万事皆有例外，比如渲染公式中就明确的定义了其中一些符号的含义：L（光照radiance）、E（辐射度irradiance）、σs（散射系数scattering coefficient）

其中，角度和标量是真实数字。向量和点由粗体小写字母标识，表示方式如下所示。在CG领域，默认均为列向量。但是有些地方使用（Vx，Vy，Vz），而非正确格式：（Vx，Vy，Vz）T，也仅仅只是为了阅读方便。

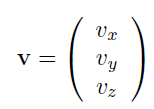
即使是使用相同的表达式，比如四分量的vector，坐标是由v = (Vx Vy Vz Vw)T表示，向量是由v = (Vx Vy Vz 0)T表示，点是由v = (Vx Vy Vz 1)T表示。然而有时，我们会使用三分量的vector表示向量/点，但是一定要尽量避免数据类型级别的误解。当进行矩阵运算的时候，向量和点使用相同的表达式非常重要。更多详情，请参照第四章：变换（Transform）。有些算法，比较喜欢使用数字索引，替代x、y、z，比如v = (V0 V1 V2)T。以上这些规则，一样适用于二分量vector，只需要简单的忽略三分量vector的最后一个成员即可。

针对矩阵运算，需要更详细的解释。常见的矩阵尺寸为2*2,3*3,4*4。我们以3*3为例进行讲解，然后可以很容易的扩展到其他类型的矩阵。矩阵中的一个标量元素为Mij，0<=(i, j) <= 2，其中i表示行，j表示列，如下所示

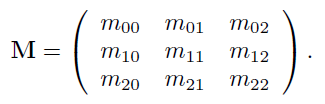
下图为使用vector的形式展示矩阵，M,j为第j列向量，Mi,为第i行向量（由于该向量是列向量，所以要加上转置符号T）。和向量、点类似，索引可以使用x、y、z、w。

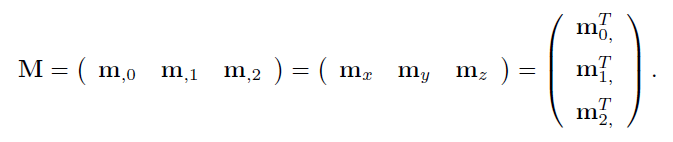
平面是通过数学公式π: n * x + d = 0表示，其中n为平面法线，表示平面的朝向；d为标量，是平面上的一个点。如果是对应曲面等，法线n为表面上某一点的法线，而针对平面，所有的点的法线都相同。平面π将整个空间分成了两半，正的一半为：n * x + d > 0；负的一半为：n * x + d < 0。其它的点都在平面上。

一个三角形，可以通过三个点定义：V0、V1、V2，然后通过ΔV0V1V2表示。

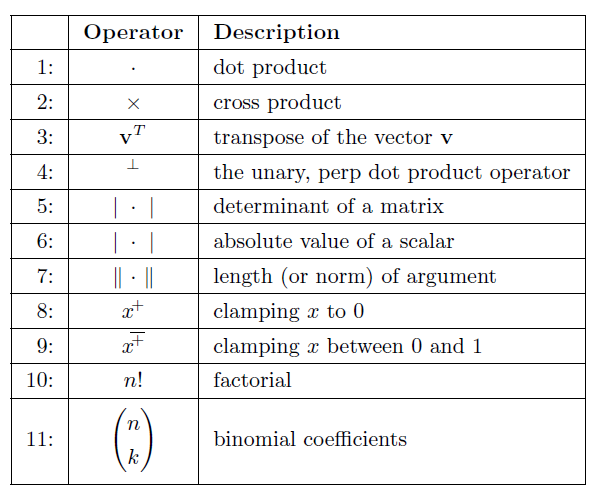
上图描述了一些运算符的意义。点积、叉积、行列式、长度运算符都可以从网站realtimerendering.com的线性代数附录中获取详细的解释。转置运算符可以将列向量转成行向量，反之亦然。第4个运算符，是在Graphics GemsIV中出现的，是一个作用于两分量vector的一元运算符，作用是获取当前vector v = (Vx Vy)T的垂直向量，即：v⊥ = (-Vy Vx)T。我们可以通过Ιa Ι来表示标量a的绝对值，或者通过 ΙA Ι表示矩阵A的行列式，当然，我们也可以通过ΙA Ι=Ι a b c Ι=det(a, b, c)来表示矩阵，其中a、b、c为矩阵的列向量。第8、9个运算符，是clamp运算符，在shader中经常会被使用，第8个运算符的目的是将负值clamp到0，第9个运算符，是将数值clamp到0到1。第10个运算符，阶乘，定义：(n! = n(n - 1)(n - 2) *** 3 * 2 * 1)，注意0!=1。第11个运算符，二项式因子，定义如下：

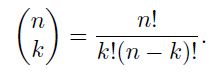
之后，我们将x = 0, y = 0, z = 0这三种平面称为坐标平面或者轴对齐平面。而轴ex = (1 0 0)T , ey = (0 1 0)T , ez = (0 0 1)T为主轴或者主方向，分别为x轴、y轴、z轴。这组轴通常被称为标准基。除非有特别说明，我们都将使用正交基（由相互垂直的单位向量组成）。

[a; b]用于表示a和b中间的值，包含a和b。(a; b)用于表示a和b中间的值，不包含a和b。[a；b）表示A和B之间的所有数字，包括A但不包括B。

文中还经常使用到atan2(y,x)。它是arctan(x)的扩展，主要区别是：-π/2 < arctan(x) < π/2 , 0 <= atan2(y; x) < 2π(Patrick：0-2pi是几个意思。。0-pi就足以了吧)。arctan的常用方式为arctan(y/x)，但是当x=0的时候，就会出现“division by zero”的错误。(Patrick：遇到过一次有意思的事情，pps的dof代码中有一段做了除0保护，也就是使用了max(x,1e-5)，但是对应的变量使用的是half的，ios上half的精度只到0.001，所以1e－5后，还是0，相当于没做除0保护。)但是如果使用atan2(y,x)就不会这样。

log(n)指的是自然对数，loge(n)，而非以10位底的对数，log10(n)

CG行业，默认3D坐标系为右手坐标系。

颜色将由三分量vector表示，比如（r,g,b），每个分量的范围为[0, 1]

1.2.2 几何定义

几乎所有的图形学硬件所使用的基本渲染图元（也被称为渲染图元）都是点、线、三角形。（我们所知道的唯一例外就是像素平面（参考文献[502]），可以绘制球体，nvdia的nv1芯片可以绘制椭圆球）

在本书中，我们将几何实体的集合看成是一个模型或者一个物件。而场景则是包含所要渲染的环境中所有模型的集合，场景还包括了材质、光照和视角信息。

一辆车、一栋建筑甚至一条线都可以被称为是一个物件。实际上，一个物件通常是由一组绘制图元组成，甚至有可能由更高类型的几何组成，比如贝塞尔曲线(Bézier curve)、曲面或者细分曲面。另外一个物件可以由其他的多个物件组成。比如汽车就是由4个门物件、4个轮子物件组成等。

1.2.3 着色

根据公认的计算机图形学用法，本书中提到的"shading"、"shader"以及相关的文字都对应着两种有区别，但是又有联系的概念：计算机生成的可视化外观（比如："shading model"、"shading equation"、"toon shading"），或者是渲染系统中的一个可编程组件（比如："vertex shader"、"shading language"）。不管是哪一种，通过上下文都应该可以很容易看出来。

1.1 内容简介

1.2 符号和定义

1.2.1 数学符号

1.2.2 几何定义

1.2.3 着色

更多资源